การวัดการกระจาย (Measures of Variability)
เป็นการหาค่าสถิติที่ใช้วัดการกระจายของคะแนนในกลุ่มเพื่อบอกให้ทราบว่าความสามารถของผู้เรียนในกลุ่มแตกต่าง
กันมากน้อยแค่ไหนถ้าการวัดการกระจายมีค่ามากแสดงว่าคะแนนของเด็กกลุ่มนั้นกระจายมาก และถ้าการวัดการกระจายมีค่า
น้อย แสดงว่าคะแนนของเด็กกระจายน้อย ถ้าการวัดการกระจาย มีค่าเป็น “ 0 ” แสดงว่าเด็กกลุ่มนั้นมีคะแนนไม่กระจายหรือ
ทุกคนได้คะแนนเท่ากัน วิธีวัดการกระจายที่นิยมใช้มี 3 ชนิด
1. พิสัย (Range) สัญลักษณ์ที่ใช้ คือ R
2. ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation) สัญลักษณ์ที่ใช้คือ S.D. หรือ S
3. ความแปรปรวน (Variance) สัญลักษณ์ที่ใช้ คือ V
พิสัย เป็นวิธีการวัดการกระจายที่ง่ายที่สุดหาได้จากความแตกต่างระหว่างคะแนนสูงสุดกับคะแนนต่ำสุด
ของข้อมูล ดังสมการ
พิสัย = คะแนนสูงสุด - คะแนนต่ำสุด
ตัวอย่าง นักเรียน 2 กลุ่ม กลุ่มละ 20 คน สอบได้คะแนนดังนี้
กลุ่มที่ 1 5,6,7,7,9,3,8,10,8,7,6,5,4,9,7,8,7,6,5,4
กลุ่มที่ 2 9,6,6,7,9,3,8,10,9,7,6,5,4,9,9,8,7,6,5,9
พิสัยกลุ่มที่ 1 = 10 – 3 = 7
พิสัยกลุ่มที่ 2 = 10 – 3 = 7
การใช้พิสัย
ค่าพิสัยของข้อมูลทั้งสองกลุ่มมีค่าเท่ากัน คือ 7 แต่การกระจายของข้อมูลที่เหลือในแต่ละกลุ่มไม่เหมือนกันดังนั้นนิยม
ใช้พิสัยในกรณีที่ต้องการดูการกระจายของข้อมูลอย่างรวดเร็ว หรือต้องการจะจัดทำตารางแจกแจงความถี่เท่านั้น
ส่วนเบี่ยงเบนมาตรฐาน
เป็นการวัดการกระจายที่ดี และใช้กันมากที่สุด มีประโยชน์ในการที่จะอนุมานค่าบางอย่างของข้อมูลแต่ละตัวจาก
ค่าเฉลี่ยมีสูตรพื้นฐานในการคำนวณดังนี้
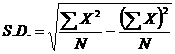
ตัวอย่าง คะแนนจากการสอบภาษาอังกฤษ 5 คน ได้คะแนนดังนี้ 3 5 9 10 12
จงหาความเบี่ยงเบนมาตรฐานของคะแนนชุดนี้
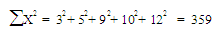
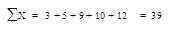
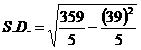
ดังนั้นส่วนเบี่ยงเบนมาตรฐาน เท่ากับ 3.31 คะแนน
การใช้ส่วนเบี่ยงเบนมาตรฐาน
1. ใช้บอกสภาพการสอบของกลุ่มควบคู่กับค่าเฉลี่ย
2. ใช้หาค่าความแปรปรวน
ความแปรปรวน คือค่าเฉลี่ยของกำลังสองของผลต่างระหว่างค่าของข้อมูลแต่ละตัว
กับค่าเฉลี่ย หรือ ความแปรปรวนคือ กำลังสองของส่วนเบี่ยงเบนมาตรฐานสูตรพื้นฐานในการคำนวณมีดังนี้
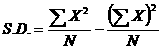
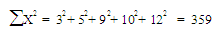
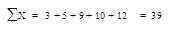
ดังนั้นส่วนเบี่ยงเบนมาตรฐาน เท่ากับ 10.95 คะแนน
สรุปการเปรียบเทียบความแตกต่างระหว่างข้อมูล 2 กลุ่ม
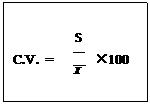
เมื่อ C.V. คือ สัมประสิทธิ์แห่งการกระจาย
S คือ ส่วนเบี่ยงเบนมาตรฐาน
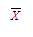 คือ ค่าเฉลี่ย
คือ ค่าเฉลี่ย